Fractales

La geometría toca todo lo que nos rodea. La ciencia es el resultado comprobable de cuestionamientos que tuvieron su origen en observaciones y cada detalle en nuestro entorno, por mínimo que sea contiene asombrosas señales sobre la manera cómo opera la naturaleza y en el caso de la geometría fractal, nos ofrece pistas que nos permiten explicar lo inexplicable: la geometría fractal.

La palabra “Fractal” señala una realidad poco aparente y esta es la existencia de un código geométrico en la naturaleza. El teorema de Pitágoras, las fórmulas para calcular superficie y volumen de las distintas figuras geométricas, el número Pi... Todos estos conceptos propios de la geometría euclidiana y la clásica, esa que se enseña - o se enseñaba- en los colegios junto a la geometría analítica que es más compleja, pues traduce las figuras a expresiones algebraicas como funciones o ecuaciones y que se adaptan a un mundo que los seres humanos han creado.

Pero, uno podría preguntarse si acaso puede existir una geometría que detrás de los patrones de comportamiento de los diferentes elementos de la naturaleza no estuviese adaptada al mundo que los humanos han creado, sino a todo lo que estaba aquí antes de que llegáramos; un mundo con una nueva perspectiva para intentar analizar y descifrar los procesos naturales que ocurren a nuestro alrededor... De eso trata la geometría fractal que ha avanzado mucho y podemos decir que llegó para quedarse, desde finales del siglo pasado.

Hace escasamente 50 años que el descubrimiento de la geometría fractal ha permitido explorar matemáticamente las “irregularidades” de la naturaleza en sus muchas de sus formas. ¿Cómo saber cuál es la lógica que siguen las ramas de un árbol cuando crecen? O la trayectoria de los rayos en una tormenta, estos y muchos fenómenos naturales se pueden desencriptar gracias a la geometría fractal.

Según principios matemáticos de autosimilitud, una misma forma se repite a escala gradualmente más pequeña de manera indefinida, es decir: una forma idéntica a si misma dentro de la anterior y así sucesivamente, hasta el infinito. Formas, ritmos, sonidos o trayectorias, porque todos estos fenómenos pueden descomponerse en estructuras autoreplicables, lo cual es la principal característica de los fractales.

En la década de los 70, Benoit Mandelbrot (1924-2010) un matemático que trabajaba para IBM en Nueva Yotk fue el responsable de acuñar en 1975 el término “FRACTAL” (del latín fractus, quebrado o fracturado). Mandelbrot nacido polaco y nacionalizado francés y estadounidense en el contexto de la II Guerra Mundial, tenía una mente excepcionalmente visual y tras su etapa como profesor en varias universidades americanas estaba empeñado en identificar por qué se producía “una interferencia de ruido blanco” en el sistema de telecomunicaciones donde trabajaba. Su dedicación le permitió encontrar la base matemática de los fractales, a pesar de que estas figuras parecían irregulares al ojo humano.

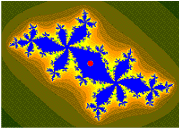
El conjunto de Mandelbrot es el más estudiado de los fractales. Este conjunto se define en el plano complejo fijando un número complejo c cualquiera, y a partir de c, se construye una sucesión por recursión que se define como el acto de una función llamándose a sí misma. La recursión es utilizada para resolver problemas que contienen subproblemas más pequeños; si la sucesión queda acotada, entonces se dice que c pertenece al conjunto de Mandelbrot, y si no, queda excluido del mismo.

Siguiendo su instinto de interpretar los problemas en términos visuales, Mandelbrot descubrió analizando las causas de “el ruido blanco” que, al margen de la escala del gráfico, los datos de un día, una hora o un segundo, tenían siempre el mismo patrón. Entonces recurrió a los trabajos de los matemáticos que habían estudiado la iteración de funciones y gracias al potencial de los ordenadores con los que trabajaba, Mandelbrot pudo replicar aquella ecuación infinitamente para obtener una de las imágenes más icónicas de la ciencia, conocida como el conjunto de Mandelbrot.

La curiosa imagen, de aspecto orgánico e irregular de los fractales es infinitamente ampliable: el patrón de los bordes se repite una y otra vez al profundizar en la imagen, respondiendo siempre al principio matemático de autosimilitud de los fractales. A grandes rasgos, un fractal es un objeto geométrico progresivo que, a partir de un patrón de repetición y escala numérica, reproduce ciertos comportamientos en la naturaleza (y su aparente caos). Años después, Mandelbrot publicó Fractal Geometry of Nature (1982) una obra con la que recibió la atención y legitimidad propias del creador de un nuevo campo de conocimiento.

Gracias al potencial de los ordenadores con los que trabajaba, Mandelbrot pudo replicar esta ecuación infinitamente para obtener una de las imágenes más icónicas de la ciencia, el conjunto de Mandelbrot. Esta curiosa imagen, de aspecto orgánico e irregular, responde al principio matemático de autosimilitud de los fractales y es infinitamente ampliable: el patrón de los bordes se repite una y otra vez al profundizar en la imagen.

El peculiar matemático (poco ortodoxo para los estándares académicos previos a su descubrimiento), defendía que los fractales son más naturales e intuitivos que los objetos basados en la Geometría Euclídea, generados y regularizados artificialmente por el hombre. Mandelbrot no fue el único responsable intelectual del nacimiento de la geometría fractal, pero sí el encargado de darle forma (literalmente) al conocimiento previo gracias al potencial de los ordenadores.

En ciencia, como en los fractales, siempre hay una forma intelectual dentro de otra más grande, aunque en este caso no se cumpla el principio de autosimilitud. Gracias al descubrimiento de los fractales, por primera vez una ecuación sencilla puede explicar formas de gran complejidad que, además, con el tiempo se ha demostrado que están presentes en los grandes procesos de la naturaleza.

Maracaibo, sábado 2 de diciembre de 2023